Recursion
What is Recursion?
Recursion is a technique where a function calls itself to solve a smaller instance of the same problem.
It is typically used when:
- The problem can be broken down into smaller subproblems.
- Each decision reduces the input size until a base case is reached.
How to Identify Recursion?
A problem is recursive if:
- We need to make
decisionsbased onchoices. - Each choice leads to a smaller input or simpler version of the problem.
- There is a
clear base case(a stopping condition) where recursion ends. - The subproblems can be combined to form the
final solution.
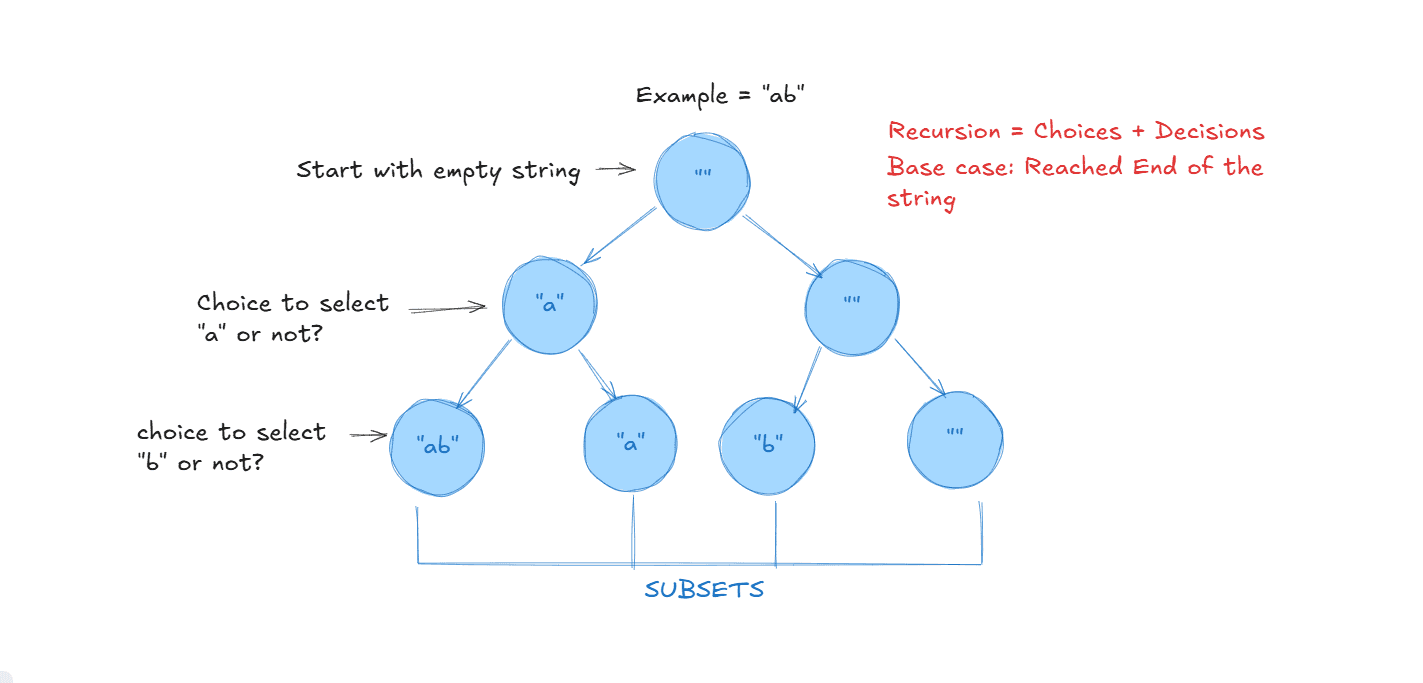
👉 Choices + Decisions = Recursion
Example: Subsequence / Substring Generation
Consider the string: const s = "abc";
Recursion is about making binary choices at each step: include or exclude each character from the original string. Exploring all such decision paths results in all possible subsequences.
Recursive Decision
For each character in the string, we recursively decide to:
Includethe character.Excludethe character.
Generating All Subsequences: Recursive Tree Approach
| Output | a | b | c |
|---|---|---|---|
| "" | ✗ | ✗ | ✗ |
| a | ✓ | ✗ | ✗ |
| b | ✗ | ✓ | ✗ |
| c | ✗ | ✗ | ✓ |
| ab | ✓ | ✓ | ✗ |
| bc | ✗ | ✓ | ✓ |
| ac | ✓ | ✗ | ✓ |
| abc | ✓ | ✓ | ✓ |
✔ = character included
✗ = character excluded
Recursion LeetCode Problems
| Problem Title | Difficulty | Description |
|---|---|---|
| Generate Parentheses | Medium | Generate all combinations of well-formed parentheses given n pairs. |
| Permutations | Medium | Return all possible permutations of a list of distinct numbers. |
| Permutations II | Medium | Return all unique permutations of a list that may contain duplicates. |
| Combinations | Medium | Generate all possible combinations of k numbers from 1 to n. |
| Subsets | Medium | Return all possible subsets (the power set) of a list of numbers. |
| Subsets II | Medium | Return all possible subsets of numbers that may contain duplicates. |
| Combination Sum | Medium | Find all unique combinations of candidates that sum to a target (reusing allowed). |
| Combination Sum II | Medium | Find all unique combinations of candidates that sum to a target (no reuse). |
| Combination Sum III | Medium | Find all valid combinations of k numbers (1–9) that sum to n. |
| Palindrome Partitioning | Medium | Partition a string into substrings such that every substring is a palindrome. |
| Restore IP Addresses | Medium | Return all possible valid IP address combinations from a string of digits. |
| Binary Watch | Medium | Return all possible times a binary watch could represent given turned-on LEDs. |